5. Block Production

5.1. Introduction

The Polkadot Host uses BABE protocol for block production. It is designed based on Ouroboros Praos. BABE execution happens in sequential non-overlapping phases known as an epoch. Each epoch is divided into a predefined number of slots. All slots in each epoch are sequentially indexed starting from 0. At the beginning of each epoch, the BABE node needs to run Block-Production-Lottery to find out in which slots it should produce a block and gossip to the other block producers. In turn, the block producer node should keep a copy of the block tree and grow it as it receives valid blocks from other block producers. A block producer prunes the tree in parallel by eliminating branches that do not include the most recently finalized blocks (Definition 5).

5.1.1. Block Producer

A block producer, noted by ${\mathcal{{P}}}_{{j}}$, is a node running the Polkadot Host, which is authorized to keep a transaction queue and which it gets a turn in producing blocks.

5.1.2. Block Authoring Session Key Pair

Block authoring session key pair ${\left({s}{{k}_{{j}}^{{s}}},{p}{{k}_{{j}}^{{s}}}\right)}$ is an SR25519 key pair which the block producer ${\mathcal{{P}}}_{{j}}$ signs by their account key (Definition 187) and is used to sign the produced block as well as to compute its lottery values in Block-Production-Lottery.

Definition 59. Epoch and Slot

A block production epoch, formally referred to as ${\mathcal{{E}}}$, is a period with a pre-known starting time and fixed-length during which the set of block producers stays constant. Epochs are indexed sequentially, and we refer to the ${n}^{{{t}{h}}}$ epoch since genesis by ${\mathcal{{E}}}_{{n}}$. Each epoch is divided into equal-length periods known as block production slots, sequentially indexed in each epoch. The index of each slot is called a slot number. The equal length duration of each slot is called the slot duration and indicated by ${\mathcal{{T}}}$. Each slot is awarded to a subset of block producers during which they are allowed to generate a block.

info

Substrate refers to an epoch as a "session" in some places. However, epoch should be the preferred and official name for these periods.

Definition 60. Epoch and Slot Duration

We refer to the number of slots in epoch ${\mathcal{{E}}}_{{n}}$ by ${s}{c}_{{n}}$. ${s}{c}_{{n}}$ is set to the duration field in the returned data from the call of the Runtime entry BabeApi_configuration (Section C.11.1.) at genesis. For a given block ${B}$, we use the notation ${s}_{{B}}$ to refer to the slot during which ${B}$ has been produced. Conversely, for slot ${s}$, ${\mathcal{{B}}}_{{c}}$ is the set of Blocks generated at slot ${s}$.

Definition 61 provides an iterator over the blocks produced during a specific epoch.

Definition 61. Epoch Subchain

By ${\text{SubChain}{\left({\mathcal{{E}}}_{{n}}\right)}}$ for epoch ${\mathcal{{E}}}_{{n}}$, we refer to the path graph of ${B}{T}$ containing all the blocks generated during the slots of epoch ${\mathcal{{E}}}_{{n}}$. When there is more than one block generated at a slot, we choose the one which is also on $\text{Longest-Chain}{\left({B}{T}\right)}$.

Definition 62. Equivocation

A block producer equivocates if they produce more than one block at the same slot. The proof of equivocation is the given distinct headers that were signed by the validator and which include the slot number.

The Polkadot Host must detect equivocations committed by other validators and submit those to the Runtime as described in Section C.11.6..

Definition 63. BABE Consensus Message

$\text{CM}_{{b}}$, the consensus message for BABE, is of the following format:

$$\text{CM}_{{b}}={\left\lbrace\begin{matrix}{1}&{\left(\text{Auth}_{{C}},{r}\right)}\\{2}&{A}_{{i}}\\{3}&{D}\end{matrix}\right.}$$

where

1	implies next epoch data: The Runtime issues this message on every first block of an epoch. The supplied authority set Definition 33, ${\text{Auth}_C}$, and randomness Definition 76, ${r}$, are used in the next epoch $\mathcal E_n + 1$. In case the epochs $\mathcal E_n + 1$ to $\mathcal E_n + k$ are skipped (i.e., BABE does not produce blocks), then the epoch data ${\left(\text{Auth}_{{C}},{r}\right)}$ is used by the epoch $\mathcal E_n + k + 1$.
2	implies on disabled: A 32-bit integer, ${A_i}$, indicating the individual authority in the current authority list that should be immediately disabled until the next authority set changes. This message's initial intention was to cause an immediate suspension of all authority functionality with the specified authority.
3	implies next epoch descriptor: These messages are only issued on configuration change and in the first block of an epoch. The supplied configuration data are intended to be used from the next epoch onwards.

• $D$ is a varying datatype of the following format:
  $$D = \{1, (c,2_{\text{nd}})\}$$
  where ${c}$ is the probability that a slot will not be empty Definition 64. It is encoded as a tuple of two unsigned 64-bit integers ${c_{nominator},c_{denominator}}$ which are used to compute the rational ${c = \frac{c_{nominator}}{c_{denominator}}}$.
• ${2_{\text{nd}}}$ describes what secondary slot Definition 67, if any, is to be used. It is encoded as one-byte varying datatype:
  $$s_{\text{2nd}} = \begin{cases} 0 \rightarrow \text{no secondary slot} \\ 1 \rightarrow \text{plain secondary slot} \\ 2 \rightarrow \text{secondary slot with VRF output} \end{cases}$$

5.2. Block Production Lottery

The BABE constant (Definition 64) is initialized at genesis to the value returned by calling BabeApi_configuration (Section C.11.1.). For efficiency reasons, it is generally updated by the Runtime through the next config data consensus message in the digest (Definition 11) of the first block of an epoch for the next epoch.

A block producer aiming to produce a block during ${\mathcal{{E}}}_{{n}}$ should run (Block-Production-Lottery) to identify the slots it is awarded. These are the slots during which the block producer is allowed to build a block. The ${s}{k}$ is the block producer lottery secret key and ${n}$ is the index of the epoch for whose slots the block producer is running the lottery.

In order to ensure consistent block production, BABE uses secondary slots in case no authority wins the (primary) block production lottery. Unlike the lottery, secondary slot assignees are known upfront publically (Definition 67). The Runtime provides information on how or if secondary slots are executed (Section C.11.1.), explained further in Definition 67.

Definition 64. BABE Constant

The BABE constant is the probability that a slot will not be empty and used in the winning threshold calculation (Definition 65). It’s expressed as a rational, ${\left({x},{y}\right)}$, where ${x}$ is the numerator and ${y}$ is the denominator.

Definition 65. Winning Threshold

The Winning threshold denoted by ${T}_{{{\mathcal{{E}}}_{{n}}}}$ is the threshold that is used alongside the result of Block-Production-Lottery to decide if a block producer is the winner of a specific slot. ${T}_{{{\mathcal{{E}}}_{{n}}}}$ is calculated as follows:

$${A}_{{w}}={\sum_{{{n}={1}}}^{{{\left|\text{Auth}_{{C}}{\left({B}\right)}\right|}}}}{\left({w}_{{A}}\in\text{Auth}_{{C}}{\left({B}\right)}_{{n}}\right)}$$

$${T}_{{{\mathcal{{E}}}_{{n}}}}\:={1}-{\left({1}-{c}\right)}^{{\frac{{w}_{{a}}}{{A}_{{w}}}}}$$

where ${A}_{{w}}$ is the total sum of all authority weights in the authority set (Definition 33) for epoch ${\mathcal{{E}}}_{{n}}$, ${w}_{{a}}$ is the weight of the block author and ${c}\in{\left({0},{1}\right)}$ is the BABE constant (Definition 64).

The numbers should be treated as 64-bit rational numbers.

5.2.1. Primary Block Production Lottery

Definition 66. BABE Slot VRF transcript, output, and proof

The BABE block production lottery requires a specific transcript structure (Definition 185). That structure is used by both primary slots (Block-Production-Lottery) and secondary slots (Definition 67).

$${t}_{{1}}\leftarrow\text{Transcript}{\left(\text{'BABE'}\right)}$$

$${t}_{{2}}\leftarrow\text{append}{\left({t}_{{1}},\text{'slot number'},{s}\right)}$$

$${t}_{{3}}\leftarrow\text{append}{\left({t}_{{2}},\text{'current epoch'},{e}_{{i}}\right)}$$

$${t}_{{4}}\leftarrow\text{append}{\left({t}_{{3}},\text{'chain randomness'},{r}\right)}$$

$${t}_{{5}}\leftarrow\text{append}{\left({t}_{{4}},\text{'vrf-nm-pk'},{p}_{{k}}\right)}$$

$${t}_{{6}}\leftarrow\text{meta-ad}{\left({t}_{{5}},\text{'VRFHash'},\text{False}\right)}$$

$${t}_{{7}}\leftarrow\text{meta-ad}{\left({t}_{{6}},{64}_{\text{le}},\text{True}\right)}$$

$${h}\leftarrow\text{prf}{\left({t}_{{7}},\text{False}\right)}$$

$${d}={s}_{{k}}\cdot{h}$$

$${\pi}\leftarrow\text{dleq\_prove}{\left({t}_{{7}},{h}\right)}$$

The operators are defined in Definition 186, $\text{dleq\_prove}$ in Definition 182. The computed outputs, ${d}$ and ${\pi}$, are included in the block Pre-Digest (Definition 74).

A block producer aiming to produce a block during ${\mathcal{{E}}}_{{n}}$ should run the $\text{Block-Production-Lottery}$ algorithm to identify the slots it is awarded. These are the slots during which the block producer is allowed to build a block. The session secret key, ${s}{k}$, is the block producer lottery secret key, and ${n}$ is the index of the epoch for whose slots the block producer is running the lottery.

Algorithm 6. Block Production Lottery

\begin{algorithm}
\caption{Block-Production-Lottery}
\begin{algorithmic}
    \require sk
    \state $r \leftarrow$ \call{Epoch-Randomness}{$n$}
    \for{$i := 1 ~\textbf{to}~ sc_n$}
        \state $(\pi, d) \leftarrow$ \call{VRF}{$r, i, sk$}
        \state $A[i] \leftarrow (d, \pi)$
    \endfor
    \return{A}
\end{algorithmic}
\end{algorithm}

where $\text{Epoch-Randomness}$ is defined in (Definition 76), ${s}{c}_{{n}}$ is defined in Definition 60 , $\text{VRF}$ creates the BABE VRF transcript (Definition 66) and ${e}_{{i}}$ is the epoch index, retrieved from the Runtime (Section C.11.1.). ${s}_{{k}}$ and ${p}_{{k}}$ is the secret key, respectively, the public key of the authority. For any slot ${s}$ in epoch ${n}$ where ${o}<{T}_{{{\mathcal{{E}}}_{{n}}}}$ (Definition 65), the block producer is required to produce a block.

info

The secondary slots (Definition 67) are running alongside the primary block production lottery and mainly serve as a fallback to in case no authority was selected in the primary lottery.

Definition 67. Secondary Slots

Secondary slots work alongside primary slot to ensure consistent block production, as described in Section 5.2.. The secondary assignee of a block is determined by calculating a specific value, ${i}_{{d}}$, which indicates the index in the authority set (Definition 33). The corresponding authority in that set has the right to author a secondary block. This calculation is done for every slot in the epoch, ${s}\in{s}{c}_{{n}}$ (Definition 60).

$${p}\leftarrow{h}{\left(\text{Enc}_{\text{SC}}{\left({r},{s}\right)}\right)}$$

$${i}_{{d}}\leftarrow{p}\text{mod}{A}_{{l}}$$

where

• ${r}$ is the Epoch randomness (Definition 76).

• ${s}$ is the slot number (Definition 59).

• $\text{Enc}_{\text{SC}}{\left(\ldots\right)}$ encodes its inner value to the corresponding SCALE value.

• ${h}{\left(\ldots\right)}$ creates a 256-bit Blake2 hash from its inner value.

• ${A}_{{l}}$ is the lengths of the authority list (Definition 33).

If ${i}_{{d}}$ points to the authority, that authority must claim the secondary slot by creating a BABE VRF transcript (Definition 66). The resulting values ${d}$ and ${\pi}$ are then used in the Pre-Digest item (Definition 74). In the case of secondary slots with plain outputs, respectively the Pre-Digest being of value 2, the transcript respectively the VRF is skipped.

5.3. Slot Number Calculation

It is imperative for the security of the network that each block producer correctly determines the current slot numbers at a given time by regularly estimating the local clock offset in relation to the network (Definition 69).

danger

The calculation described in this section is still to be implemented and deployed: For now, each block producer is required to synchronize its local clock using NTP instead. The current slot ${s}$ is then calculated by ${s}={t}_{\text{unix}}/{\mathcal{{T}}}$ where ${\mathcal{{T}}}$ is defined in Definition 59 and ${t}_{\text{unix}}$ is defined in Definition 191. That also entails that slot numbers are currently not reset at the beginning of each epoch.

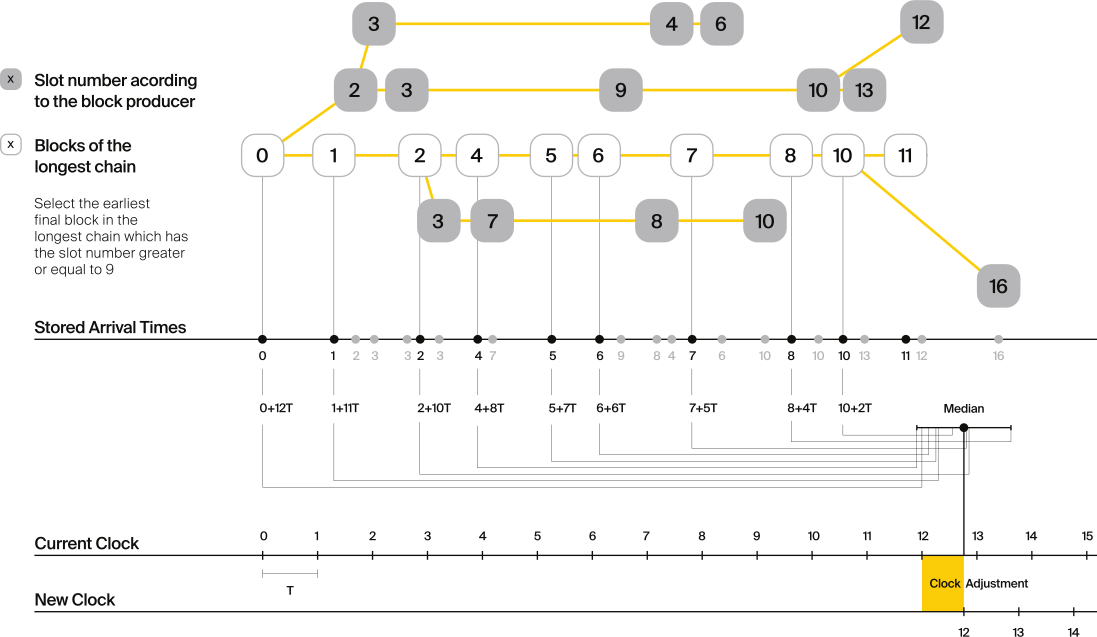
Using the median algorithm described in this section, Polkadot achieves synchronization without relying on any external clock source (e.g., through the NTP or GPS protocol). To stay in synchronization, each producer is therefore required to periodically estimate its local clock offset in relation to the rest of the network.

This estimation depends on the two fixed parameters ${k}$ (Definition 70) and ${s}_{{{c}{q}}}$ (Definition 71). These are chosen based on the results of a formal security analysis, currently assuming a ${1}{s}$ clock drift per day and targeting a probability lower than ${0.5}\%$ for an adversary to break BABE in 3 years with resistance against a network delay up to $\frac{{1}}{{3}}$ of the slot time and a BABE constant (Definition 64) of ${c}={0.38}$.

All validators are then required to run Median-Algorithm at the beginning of each sync period (Definition 73) to update their synchronization using all block arrival times of the previous period. The algorithm should only be run once all the blocks in this period have been finalized, even if only probabilistically (Definition 70). The target slot to which to synchronize should be the first slot in the new sync period.

Definition 68. Slot Offset

Let ${s}_{{i}}$ and ${s}_{{j}}$ be two slots belonging to epochs ${\mathcal{{E}}}_{{k}}$ and ${\mathcal{{E}}}_{{l}}$. By Slot-Offset${\left({s}_{{i}},{s}_{{j}}\right)}$ we refer to the function whose value is equal to the number of slots between ${s}_{{i}}$ and ${s}_{{j}}$ (counting ${s}_{{j}}$) on the time continuum. As such, we have Slot-Offset${\left({s}_{{i}},{s}_{{i}}\right)}={0}$.

It is imperative for the security of the network that each block producer correctly determines the current slot numbers at a given time by regularly estimating the local clock offset in relation to the network (Definition 69).

Definition 69. Relative Time Synchronization

The relative time synchronization is a tuple of a slot number and a local clock timestamp ${\left({s}_{\text{sync}},{t}_{\text{sync}}\right)}$ describing the last point at which the slot numbers have been synchronized with the local clock.

Algorithm 7. Slot Time

\begin{algorithm}
\caption{Slot-Time}
\begin{algorithmic}
    \require $s$
    \return{$t_\text{sync} + $\call{Slot-Offset}{$s_{sync}, s$}$ \times \mathcal{T}$}
\end{algorithmic}
\end{algorithm}

where ${s}$ is the slot number.

Algorithm 8. Median Algorithm

\begin{algorithm}
\caption{Median-Algorithm}
\begin{algorithmic}
    \require $\mathfrak{E}, s_{sync}$
    \state $T_s \leftarrow \{ \}$
    \for{$B ~\textbf{in}~ \mathfrak{E}_j$}
        \state $t_{est}^{B} \leftarrow T_B + $\call{Slot-Offset}{$s_B, s_{sync}$}$ \times \mathcal{T}$
        \state $T_s \leftarrow T_s \cup t_{est}^{B}$
    \endfor
    \return \call{Median}{$T_s$}
\end{algorithmic}
\end{algorithm}

where

• ${\mathfrak{{{E}}}}$ is the sync period used for the estimate.

• ${s}_{\text{sync}}$ is the slot time to estimate.

• $\text{Slot-Offset}$ is defined in Slot-Time.

• ${\mathcal{{{T}}}}$ is the slot duration defined in Definition 59.

Definition 70. Pruned Best Chain

The pruned best chain ${C}^{{{r}^{{k}}}}$ is the longest selected chain (Definition 7) with the last ${k}$ Blocks pruned. We chose ${k}={140}$. The last (probabilistic) finalized block describes the last block in this pruned best chain.

Definition 71. Chain Quality

The chain quality ${s}_{{{c}{q}}}$ represents the number of slots that are used to estimate the local clock offset. Currently, it is set to ${s}_{{{c}{q}}}={3000}$.

The prerequisite for such a calculation is that each producer stores the arrival time of each block (Definition 72) measured by a clock that is otherwise not adjusted by any external protocol.

Definition 72. Block Arrival Time

The block arrival time of block ${B}$ for node ${j}$ formally represented by ${{T}_{{B}}^{{j}}}$ is the local time of node ${j}$ when node ${j}$ has received block ${B}$ for the first time. If the node ${j}$ itself is the producer of ${B}$, ${{T}_{{B}}^{{j}}}$ is set equal to the time that the block is produced. The index ${j}$ in ${{T}_{{B}}^{{j}}}$ notation may be dropped, and B’s arrival time is referred to by ${T}_{{B}}$ when there is no ambiguity about the underlying node.

Definition 73. Sync Period

A is an interval at which each validator (re-)evaluates its local clock offsets. The first sync period ${\mathfrak{{E}}}_{{1}}$ starts just after the genesis block is released. Consequently, each sync period ${\mathfrak{{E}}}_{{i}}$ starts after ${\mathfrak{{E}}}_{{{i}-{1}}}$. The length of the sync period (Definition 71) is equal to ${s}_{{{q}{c}}}$and expressed in the number of slots.

Image 5. An exemplary result of Median Algorithm in first sync epoch with ${s}_{\text{cq}}={9}$ and ${k}={1}$.

5.4. Production Algorithm

Throughout each epoch, each block producer should run Invoke-Block-Authoring to produce blocks during the slots it has been awarded during that epoch. The produced block needs to carry the Pre-Digest (Definition 74) as well as the block signature (Definition 75) as Pre-Runtime and Seal digest items.

Definition 74. Pre-Digest

The Pre-Digest, or BABE header, ${P}$, is a varying datatype of the following format:

$${P}={\left\lbrace\begin{matrix}{1}&\rightarrow&{\left({a}_{\text{id}},{s},{d},{\pi}\right)}\\{2}&\rightarrow&{\left({a}_{\text{id}},{s}\right)}\\{3}&\rightarrow&{\left({a}_{\text{id}},{s},{d},{\pi}\right)}\end{matrix}\right.}$$

where

• 1 indicates a primary slot with VRF outputs, 2 a secondary slot with plain outputs and 3 a secondary slot with VRF outputs (Section 5.2.). Plain outputs are no longer actively used and only exist for backwards compatibility reasons, respectively to sync old blocks.

• ${a}_{\text{id}}$ is the unsigned 32-bit integer indicating the index of the authority in the authority set (Section 3.3.1.) who authored the block.

• ${s}$ is the slot number (Definition 59).

• ${d}$ is VRF output (Block-Production-Lottery respectively Definition 67).

• ${\pi}$ is VRF proof (Block-Production-Lottery respectively Definition 67).

The Pre-Digest must be included as a digest item of Pre-Runtime type in the header digest (Definition 11) ${H}_{{d}}{\left({B}\right)}$.

Algorithm 9. Invoke-Block-Authoring

\begin{algorithm}
\caption{Invoke-Block-Authoring}
\begin{algorithmic}
    \require $sk, pk, n, BT$
    \state $A \leftarrow$ \call{Block-production-lottery}{$sk, n$}
    \for{$s \leftarrow 1 ~\textbf{to}~ sc_n$}
        \state \call{Wait-Until}{\call{Slot-Time}{$s$}}
        \state $(d, \pi) \leftarrow A[s]$
        \if{$\tau > d$}
            \state $C_{Best} \leftarrow$ \call{Longest-Chain}{$BT$}
            \state $B_s \leftarrow$ \call{Build-Block}{$C_{Best}$}
            \state \call{Add-Digest-Item}{$B_s,\text{Pre-Runtime}, E_{id}(\text{BABE}), H_\text{BABE}(B_s)$}
            \state \call{Add-Digest-Item}{$B_s, \text{Seal}, S_B$}
            \state \call{Broadcast-Block}{$B_s$}
        \endif
    \endfor
\end{algorithmic}
\end{algorithm}

where $\text{BT}$ is the current block tree, $\text{Block-Production-Lottery}$ is defined in Block-Production-Lottery and $\text{Add-Digest-Item}$ appends a digest item to the end of the header digest ${H}_{{d}}{\left({B}\right)}$ (Definition 11).

Definition 75. Block Signature

The Block Signature ${S}_{{B}}$ is a signature of the block header hash (Definition 12) and defined as

$$\text{Sig}_{{\text{SR25519},{\text{sk}_{{j}}^{{s}}}}}{\left({H}_{{h}}{\left({B}\right)}\right)}$$

${m}$ should be included in ${H}_{{d}}{\left({B}\right)}$ as the Seal digest item (Definition 11) of value:

$${\left({t},\text{id}{\left(\text{BABE}\right)},{m}\right)}$$

in which, ${t}={5}$ is the seal digest identifier and $\text{id}{\left(\text{BABE}\right)}$ is the BABE consensus engine unique identifier (Definition 11). The Seal digest item is referred to as the BABE Seal.

5.5. Epoch Randomness

At the beginning of each epoch, ${\mathcal{{E}}}_{{n}}$ the host will receive the randomness seed ${\mathcal{{R}}}_{{{\mathcal{{E}}}_{{{n}+{1}}}}}$ (Definition 76) necessary to participate in the block production lottery in the next epoch ${\mathcal{{E}}}_{{{n}+{1}}}$ from the Runtime, through the consensus message (Definition 63) in the digest of the first block.

Definition 76. Randomness Seed

For epoch ${\mathcal{{E}}}$, there is a 32-byte ${\mathcal{{R}}}_{{{\mathcal{{E}}}}}$ computed based on the previous epochs VRF outputs. For ${\mathcal{{E}}}_{{0}}$ and ${\mathcal{{E}}}_{{1}}$, the randomness seed is provided in the genesis state (Section C.11.1.). For any further epochs, the randomness is retrieved from the consensus message (Definition 63).

5.6. Verifying Authorship Right

When a Polkadot node receives a produced block, it needs to verify if the block producer was entitled to produce the block in the given slot by running Verify-Authorship-Right. Verify-Slot-Winner runs as part of the verification process, when a node is importing a block.

Algorithm 10. Verify Authorship Right

\begin{algorithm}
\caption{Verify-Authorship-Right}
\begin{algorithmic}
    \require $\text{Head}_{s(B)}$
    \state $s \leftarrow$ \call{Slot-Number-At-Given-Time}{$T_B$}
    \state $\mathcal{E}_c \leftarrow$ \call{Current-Epoch}{}
    \state $(D_1, \ldots, D_{|H_d(B)|}) \leftarrow H_d(B)$
    \state $D_s \leftarrow D_{|H_d(B)|}$
    \state $H_d(B) \leftarrow \left(D_1, \ldots, D_{|H_d(B)| - 1}\right)$
        \comment{remove the seal from the digest}
    \state $(id, \text{Sig}_B)\leftarrow \text{Dec}_{SC}(D_s)$
    \if{$id \neq$ \textsc{Seal-Id}}
        \state \textbf{error} ``Seal missing''
    \endif
    \state $\text{AuthorID} \leftarrow \text{AuthorityDirectory}^{\mathcal{E}_c}[H_{BABE}(B).\text{SingerIndex}]$
    \state \call{Verify-Signature}{$\text{AuthorID}, H_h(B),\text{Sig}_B$}
    \if{$\exists B' \in BT : H_h(B) \neq H_h (B)$ \and $s_B = s_B'$ \and $\text{SignerIndex}_B = \text{SignerIndex}_{B'}$}
        \state \textbf{error} ``Block producer is equivocating''
    \endif
    \state \call{Verify-Slot-Winner}{$(d_B, \pi_B), s_B, \text{AuthorID}$}
\end{algorithmic}
\end{algorithm}

where

• $\text{Head}_{{s}}{\left({B}\right)}$ is the header of the block that’s being verified.

• ${T}_{{B}}$ is ${B}$’s arrival time (Definition 72).

• ${H}_{{d}}{\left({B}\right)}$ is the digest sub-component (Definition 11) of $\text{Head}{\left({B}\right)}$ (Definition 10).

• The Seal ${D}_{{s}}$ is the last element in the digest array ${H}_{{d}}{\left({B}\right)}$ as described in Definition 11.

• $\text{Seal-Id}$ is the type index showing that a digest item (Definition 11) of varying type (Definition 199) is of type Seal.

• $\text{AuthorityDirectory}^{{{\mathcal{{E}}}_{{c}}}}$ is the set of Authority ID for block producers of epoch ${\mathcal{{E}}}_{{c}}$.

  1. $\text{AuthorId}$ is the public session key of the block producer.

• $\text{BT}$ is the pruned block tree (Definition 5).

• $\text{Verify-Slot-Winner}$ is defined in Verify-Slot-Winner.

Algorithm 11. Verify Slot Winner

\begin{algorithm}
\caption{Verify-Slot-Winner}
\begin{algorithmic}
    \require $B$
    \state $\mathcal{E}_c \leftarrow$ \textsc{Current-Epoch}
    \state $\rho \leftarrow$ \call{Epoch-Randomness}{$c$}
    \state \call{Verify-VRF}{$\rho, H_{BABE}(B).(d_B, \pi_B), H_{BABE}(B).s, c$}
    \if{$d_B \geqslant \tau$}
        \state \textbf{error} ``Block producer is not a winner of the slot''
    \endif
\end{algorithmic}
\end{algorithm}

where

1. $\text{Epoch-Randomness}$ is defined in Definition 76.

2. ${H}_{\text{BABE}}{\left({B}\right)}$ is the BABE header defined in Definition 74.

3. ${\left({o},{p}\right)}$ is the block lottery result for block ${B}$ (Block-Production-Lottery), respectively the VRF output (Definition 66).

4. $\text{Verify-VRF}$ is described in Section A.1.3..

5. ${T}_{{{\mathcal{{E}}}_{{n}}}}$ is the winning threshold as defined in Definition 65.

5.7. Block Building Process

The block building process is triggered by Invoke-Block-Authoring of the consensus engine which in turn runs Build-Block.

Algorithm 12. Build Block

\begin{algorithm}
\caption{Build-Block}
\begin{algorithmic}
    \state $P_B \leftarrow $\call{Head}{$C_{Best}$}
    \state $\text{Head}(B) \leftarrow \left(H_p \leftarrow H_h(P_B), H_i \leftarrow H_i(P_B) + 1, H_r \leftarrow \phi, H_e \leftarrow \phi, H_d \leftarrow \phi \right)$
    \state \call{Call-Runtime-Entry}{$\texttt{Core\_initialize\_block}, \text{Head}(B)$}
    \state \textsc{I-D}$ \leftarrow $\call{Call-Runtime-Entry}{$\texttt{BlockBuilder\_inherent\_extrinsics}, $\textsc{Inherent-Data}}
    \for{$E~\textbf{in} $\textsc{I-D}}
        \state \call{Call-Runtime-Entry}{$\texttt{BlockBuilder\_apply\_extrinsics}, E$}
    \endfor
    \while{\not \call{End-Of-Slot}{$s$}}
        \state $E \leftarrow$ \call{Next-Ready-Extrinsic}{}
        \state $R \leftarrow$ \call{Call-Runtime-Entry}{$\texttt{BlockBuilder\_apply\_extrinsics}, E$}
        \if{\call{Block-Is-Full}{$R$}}
            \break
        \endif
        \if{\call{Should-Drop}{$R$}}
            \state \call{Drop}{$E$}
        \endif
        \state $\text{Head}(B) \leftarrow$ \call{Call-Runtime-Entry}{$\texttt{BlockBuilder\_finalize\_block}, B$}
        \state $B \leftarrow$ \call{Add-Seal}{$B$}
    \endwhile
\end{algorithmic}
\end{algorithm}

where

• ${C}_{\text{Best}}$ is the chain head at which the block should be constructed ("parent").

• ${s}$ is the slot number.

• $\text{Head}{\left({B}\right)}$ is defined in Definition 10.

• $\text{Call-Runtime-Entry}$ is defined in Definition 32.

• $\text{Inherent-Data}$ is defined in Definition 15.

• $\text{End-Of-Slot}$ indicates the end of the BABE slot as defined Median-Algorithm respectively Definition 59.

• $\text{Next-Ready-Extrinsic}$ indicates picking an extrinsic from the extrinsics queue (Definition 14).

• $\text{Block-Is-Full}$ indicates that the maximum block size is being used.

• $\text{Should-Drop}$ determines based on the result ${R}$ whether the extrinsic should be dropped or remain in the extrinsics queue and scheduled for the next block. The ApplyExtrinsicResult (Definition 230) describes this behavior in more detail.

• $\text{Drop}$ indicates removing the extrinsic from the extrinsic queue (Definition 14).

• $\text{Add-Seal}$ adds the seal to the block (<<>>) before sending it to peers. The seal is removed again before submitting it to the Runtime.