6. Finality

6.1. Introduction

The Polkadot Host uses GRANDPA Finality protocol to finalize blocks. Finality is obtained by consecutive rounds of voting by the validator nodes. Validators execute GRANDPA finality process in parallel to Block Production as an independent service. In this section, we describe the different functions that GRANDPA service performs to successfully participate in the block-finalization process.

Definition 77. GRANDPA Voter

A GRANDPA Voter, ${v}$, represented by a key pair ${\left({{K}_{{v}}^{{\text{pr}}}},{v}_{{\text{id}}}\right)}$ where ${{k}_{{v}}^{{\text{pr}}}}$ represents an ed25519 private key, is a node running a GRANDPA protocol and broadcasting votes to finalize blocks in a Polkadot Host-based chain. The set of all GRANDPA voters for a given block B is indicated by ${\mathbb{{V}}}_{{B}}$. In that regard, we have [To do: change function name, only call at genesis, adjust V_B over the sections]

$${\mathbb{{V}}}={\tt{grandpa\_authorities}}{\left({B}\right)}$$

where ${\tt{grandpa\_authorities}}$ is a function entry point of the Runtime described in Section C.10.1.. We refer to ${\mathbb{{V}}}_{{B}}$ as ${\mathbb{{V}}}$ when there is no chance of ambiguity.

Analogously, we say that a Polkadot node is a non-voter node for block ${B}$ if it does not own any of the key pairs in ${\mathbb{{V}}}_{{B}}$.

Definition 78. Authority Set Id

The authority set Id ($\text{id}_{{{\mathbb{{V}}}}}$) is an incremental counter which tracks the amount of authority list changes that occurred (Definition 91). Starting with the value of zero at genesis, the Polkadot Host increments this value by one every time a Scheduled Change or a Forced Change occurs. The authority set ID is an unsigned 64-bit integer.

Definition 79. GRANDPA State

The GRANDPA state, $\text{GS}$, is defined as:

$$\text{GS}\:={\left\lbrace{\mathbb{{V}}},\text{id}_{{{\mathbb{{V}}}}},{r}\right\rbrace}$$

where

• ${\mathbb{{V}}}$: is the set of voters.

• $\text{id}_{{{\mathbb{{V}}}}}$: is the authority set ID (Definition 78).

• ${r}$: is the voting round number.

Definition 80. GRANDPA Vote

A GRANDPA vote or simply a vote for block ${B}$ is an ordered pair defined as

$${V}{\left({B}\right)}\:={\left({H}_{{h}}{\left({B}\right)},{H}_{{i}}{\left({B}\right)}\right)}$$

where ${H}_{{h}}{\left({B}\right)}$ and ${H}_{{i}}{\left({B}\right)}$ are the block hash (Definition 12) and the block number (Definition 10).

Definition 81. Voting Rounds

Voters engage in a maximum of two sub-rounds of voting for each round ${r}$. The first sub-round is called pre-vote, and the second is called pre-commit.

By ${{V}_{{v}}^{{{r},\text{pv}}}}$ and ${{V}_{{v}}^{{{r},\text{pc}}}}$ we refer to the vote cast by voter ${v}$ in round ${r}$ (for block ${B}$) during the pre-vote and the pre-commit sub-round respectively.

Voting is done by means of broadcasting voting messages (Section 4.8.7.) to the network. Validators inform their peers about the block finalized in round ${r}$ by broadcasting a commit message (Play-Grandpa-Round).

Definition 82. Vote Signature

${\text{Sign}_{{{v}_{{i}}}}^{{{r},\text{stage}}}}$ refers to the signature of a voter for a specific message in a round and is formally defined as:

$${\text{Sign}_{{{v}_{{i}}}}^{{{r},\text{stage}}}}\:=\text{Sig}_{{\text{ed25519}}}{\left(\text{msg},{r},\text{id}_{{{\mathbb{{V}}}}}\right)}$$

where

• $\text{msg}$: is a byte array containing the message to be signed (Definition 80).

• ${r}$: is an unsigned 64-bit integer is the round number.

• $\text{id}_{{{\mathbb{{V}}}}}$: is an unsigned 64-bit integer indicating the authority set Id (Definition 78).

• $\text{stage}$: is either the pre-vote (${stage = pv}$) or the pre-commit (${stage = pc}$) sub-round of voting ${r}$, as defined in (Definition 81).

Definition 83. Justification

The justification for block ${B}$ in round ${r}$, ${J}^{{{r},\text{stage}}}{\left({B}\right)}$, is a vector of pairs of the type:

$${\left({V}{\left({B}'\right)},{\text{Sign}_{{{v}_{{i}}}}^{{{r},\text{stage}}}}{\left({B}'\right)},{v}_{{\text{id}}}\right)}$$

in which either

${B}'\ge{B}$

or ${{V}_{{{v}_{{i}}}}^{{{r},\text{pc}}}}{\left({B}'\right)}$ is an equivocatory vote.

In all cases, ${\text{Sign}_{{{v}_{{i}}}}^{{{r},\text{stage}}}}{\left({B}'\right)}$ is the signature (Definition 82) of voter ${v}_{{\text{id}}}\in{\mathbb{{V}}}_{{B}}$ broadcasted during a specific ${stage}$ (i.e., sub-round)(Definition 81) of round r. A valid justification must only contain up to one valid vote from each voter and must not contain more than two equivocatory votes from each voter.

Definition 84. Finalizing Justification

We say ${J}^{{{r},\text{pc}}}{\left({B}\right)}$ justifies the finalization of ${B}'\ge{B}$ for a non-voter node ${n}$ if the number of valid signatures in ${J}^{{{r},\text{pc}}}{\left({B}\right)}$ for ${B}'$ is greater than $\frac{{2}}{{3}}{\left|{\mathbb{{V}}}_{{B}}\right|}$.

Note that ${J}^{{{r},\text{pc}}}{\left({B}\right)}$ can only be used by a non-voter node to finalize a block. In contrast, a voter node can only be assured of the finality (Definition 94) of block ${B}$ by actively participating in the voting process. That is by invoking Play-Grandpa-Round.

The GRANDPA protocol dictates how an honest voter should vote in each sub-round, which is described by Play-Grandpa-Round. After defining what constitutes a vote in GRANDPA, we define how GRANDPA counts votes.

Definition 85. Equivocation

Voter ${v}$ equivocates if they broadcast two or more valid votes to blocks during one voting sub-round. In such a situation, we say that ${v}$ is an equivocator and any vote ${{V}_{{v}}^{{{r},\text{stage}}}}{\left({B}\right)}$ cast by ${v}$ in that sub-round is an equivocatory vote, and

$${\mathcal{{E}}}^{{{r},\text{stage}}}$$

represents the set of all equivocators voters in sub-round stage of round ${r}$. When we want to refer to the number of equivocators whose equivocation has been observed by voter ${v}$, we refer to it by:

$${{\mathcal{{E}}}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}$$

The Polkadot Host must detect equivocations committed by other validators and submit those to the Runtime as described in Section C.10.3..

A vote ${{V}_{{v}}^{{{r},\text{stage}}}}={V}{\left({B}\right)}$ is invalid if

• ${H}{\left({B}\right)}$ does not correspond to a valid block.

• ${B}$ is not an (eventual) descendant of a previously finalized block.

• ${{M}_{{v}}^{{{r},\text{stage}}}}$ does not bear a valid signature.

• $\text{id}_{{{\mathbb{{V}}}}}$ does no match the current ${\mathbb{{V}}}$.

• ${{V}_{{v}}^{{{r},\text{stage}}}}$ is an equivocatory vote.

Definition 86. Set of Observed Direct Votes

For validator ${v}$, the set of observed direct votes for Block ${B}$ in round ${r}$, formally denoted by ${\text{VD}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}{\left({B}\right)}$ is equal to the union of:

• set of valid votes ${{V}_{{{v}_{{i}}}}^{{{r},\text{stage}}}}$ cast in round ${r}$ and received by ${v}$ such that ${{V}_{{{v}_{{i}}}}^{{{r},\text{stage}}}}={V}{\left({B}\right)}$.

Definition 87. Set of Total Observed Votes

We refer to the set of total votes observed by voter ${v}$ in sub-round stage of round ${r}$ by ${{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}$.

The set of all observed votes by ${v}$ in the sub-round stage of round ${r}$ for block ${B}$, ${{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}$ is equal to all of the observed direct votes cast for block ${B}$ and all of the ${B}$’s descendants defined formally as:

$${{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}{\left({B}\right)}\:=\bigcup_{{{v}_{{i}}\in{\mathbb{{V}}},{B}<{B}'}}{\text{VD}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}{\left({B}'\right)}$$

The total number of observed votes for Block ${B}$ in round ${r}$ is defined to be the size of that set plus the total number of equivocator voters:

$${{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}{\left({B}\right)}\:={\left|{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}{\left({B}\right)}\right|}+{\left|{{\mathcal{{E}}}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}\right|}$$

Note that for genesis state we always have $\#{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{pv}}}}{\left({B}\right)}={\left|{\mathbb{{V}}}\right|}$.

Definition 88. Set of Total Potential Votes

Let ${{V}_{{\text{unobs}{\left({v}\right)}}}^{{{r},\text{stage}}}}$ be the set of voters whose vote in the given stage has not been received. We define the total number of potential votes for Block ${B}$ in round ${r}$ to be:

$$\#{{V}_{{\text{obs}{\left({v}\right)},\text{pot}}}^{{{r},\text{stage}}}}{\left({B}\right)}\:={\left|{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}{\left({B}\right)}\right|}+{\left|{{V}_{{\text{unobs}{\left({v}\right)}}}^{{{r},\text{stage}}}}\right|}+\text{Min}{\left(\frac{{1}}{{3}}{\left|{\mathbb{{V}}}\right|},{\left|{\mathbb{{V}}}\right|}-{\left|{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{stage}}}}{\left({B}\right)}\right|}-{\left|{{V}_{{\text{unobs}{\left({v}\right)}}}^{{{r},\text{stage}}}}\right|}\right)}$$

Definition 89. Current Pre-Voted Block

The current pre-voted block ${{B}_{{v}}^{{{r},\text{pv}}}}$ also known as GRANDPA GHOST is the block chosen by GRANDPA-GHOST:

$${{B}_{{v}}^{{{r},\text{pv}}}}\:=\text{GRANDPA-GHOST}{\left({r}\right)}$$

Finally, we define when a voter ${v}$ sees a round as completable, that is, when they are confident that ${{B}_{{v}}^{{{r},\text{pv}}}}$ is an upper bound for what is going to be finalized in this round.

Definition 90. Completable Round

We say that round ${r}$ is completable if ${\left|{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{pc}}}}\right|}+{{\mathcal{{E}}}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{pc}}}}>\frac{{2}}{{3}}{\mathbb{{V}}}$ and for all ${B}'>{{B}_{{v}}^{{{r},\text{pv}}}}$:

$${\left|{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{pc}}}}\right|}-{{\mathcal{{E}}}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{pc}}}}-{\left|{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{pc}}}}{\left({B}'\right)}\right|}>\frac{{2}}{{3}}{\left|{\mathbb{{V}}}\right|}$$

Note that in practice we only need to check the inequality for those ${B}'>{{B}_{{v}}^{{{r},\text{pv}}}}$ where ${\left|{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},\text{pc}}}}{\left({B}'\right)}\right|}>{0}$.

Definition 91. GRANDPA Consensus Message

$\text{CM}_{{g}}$, the consensus message for GRANDPA, is of the following format:

$$\text{CM}_{{g}}={\left\lbrace\begin{matrix}{1}&{\left(\text{Auth}_{{C}},{N}_{{\text{delay}}}\right)}\\{2}&{\left({m},\text{Auth}_{{C}},{N}_{{\text{delay}}}\right)}\\{3}&\text{A}_{{i}}\\{4}&{N}_{{\text{delay}}}\\{5}&{N}_{{\text{delay}}}\end{matrix}\right.}$$

where

$N_{\text{delay}}$	is an unsigned 32-bit integer indicating how deep in the chain the announcing block must be before the change is applied.
1	Implies scheduled change: Schedule an authority set change after the given delay of ${N_{\text{delay}} := \|\text{SubChain}(B,B')\|}$ where ${B'}$ is the block where the change is applied. The earliest digest of this type in a single block will be respected, unless a force change is present, in which case the force change takes precedence.
2	Implies forced change: Schedule a forced authority set change after the given delay of ${N_{\text{delay}} := \|\text{SubChain}(B,m + B')\|}$ where ${B'}$ is the block where the change is applied. The earliest digest of this type in a block will be respected. Forced changes are explained further in Section 6.5..
3	Implies on disabled: An index to the individual authority in the current authority list (Definition 33) that should be immediately disabled until the next authority set changes. When an authority gets disabled, the node should stop performing any authority functionality from that authority, including authoring blocks and casting GRANDPA votes for finalization. Similarly, other nodes should ignore all messages from the indicated authority which pertain to their authority role.
4	Implies pause: A signal to pause the current authority set after the given delay of ${N_{\text{delay}} := \|\text{SubChain}(B,B')\|}$ where ${B'}$ is a block where the change is applied. Once applied, the authorities should stop voting.
5	Implies resume: A signal to resume the current authority set after the given delay of ${N_{\text{delay}} := \|\text{SubChain}(B,B')\|}$ where ${B'}$ is the block where the change is applied. Once applied, the authorities should resume voting.

6.2. Initiating the GRANDPA State

In order to participate coherently in the voting process, a validator must initiate its state and sync it with other active validators. In particular, considering that voting is happening in different distinct rounds where each round of voting is assigned a unique sequential round number ${r}_{{v}}$, it needs to determine and set its round counter ${r}$ equal to the voting round ${r}_{{n}}$ currently undergoing in the network. The mandated initialization procedure for the GRANDPA protocol for a joining validator is described in detail in Initiate-Grandpa.

The process of joining a new voter set is different from the one of rejoining the current voter set after a network disconnect. The details of this distinction are described further in this section.

6.2.1. Voter Set Changes

A GRANDPA voter node which is initiating GRANDPA protocol as part of joining a new authority set is required to execute Initiate-Grandpa. The algorithm mandates the initialization procedure for GRANDPA protocol.

info

The GRANDPA round number reset to 0 for every authority set change.

Voter set changes are signaled by Runtime via a consensus engine message (Section 3.3.2.). When Authorities process such messages they must not vote on any block with a higher number than the block at which the change is supposed to happen. The new authority set should reinitiate GRANDPA protocol by executing Initiate-Grandpa.

Algorithm 13. Initiate Grandpa

\begin{algorithm}
\caption{Initiate-Grandpa}
\begin{algorithmic}
    \input $r_{last}, B_{last}$
    \state \textsc{Last-Finalized-Block} $\leftarrow B_{last}$
    \state \textsc{Best-Final-Candidate}$(0) \leftarrow B_{last}$
    \state \textsc{GRANDPA-GHOST}$(0) \leftarrow B_{last}$
    \state \textsc{Last-Completed-Round}$ \leftarrow 0$
    \state $r_n \leftarrow 1$
    \state \call{Play-Grandpa-round}{$r_n$}
\end{algorithmic}
\end{algorithm}

where ${B}_{{\text{last}}}$ is the last block which has been finalized on the chain (Definition 94). ${r}_{{\text{last}}}$ is equal to the latest round the voter has observed that other voters are voting on. The voter obtains this information through various gossiped messages including those mentioned in Definition 94. ${r}_{{\text{last}}}$ is set to 0 if the GRANDPA node is initiating the GRANDPA voting process as a part of a new authority set. This is because the GRANDPA round number resets to 0 for every authority set change.

6.3. Rejoining the Same Voter Set

When a voter node rejoins the network after a disconnect from the voter set and with the condition that there has been no change to the voter set at the time of the disconnect, the node must continue performing the GRANDPA protocol at the same state as before getting disconnected from the network, ignoring any possible progress in GRANDPA finalization. Following reconnection, the node eventually gets updated to the current GRANDPA round and synchronizes its state with the rest of the voting set through the process called Catchup (Section 6.6.1.).

6.4. Voting Process in Round ${r}$

For each round ${r}$, an honest voter ${v}$ must participate in the voting process by following Play-Grandpa-Round.

Algorithm 14. Play Grandpa Round

\begin{algorithm}
\caption{Play-Grandpa-Round}
\begin{algorithmic}
    \REQUIRE($r$)
    \STATE $t_{r, v} \leftarrow$ Current local time
    \STATE $\textrm{primary} \leftarrow$ \call{Derive-Primary}{$r$}
    \IF{$v = \textrm{primary}$}
      \STATE \call{Broadcast}{$M_{v}^{r - 1, \textrm{Fin}}($\call{Best-Final-Candidate}{$r - 1$}$)$}
      \IF{\call{Best-Final-Candidate}{$r - 1$} $\geqslant$ \textsc{Last-Finalized-Block}}
        \STATE \call{Broadcast}{$M_{v}^{r - 1, \textrm{Prim}}($\call{Best-Final-Candidate}{$r - 1$}$)$}
      \ENDIF
    \ENDIF
    \STATE \call{Receive-Messages}{\textbf{until} Time $\geqslant t_{r_,v} + 2 \times T$ \or $r$ \textbf{is} completable}
    \STATE $L \leftarrow$ \call{Best-Final-Candidate}{$r - 1$}
    \STATE $N \leftarrow$ \call{Best-PreVote-Candidate}{$r$}
    \STATE \call{Broadcast}{$M_v^{r, \textrm{pv}} (N)$}
    \STATE \call{Receive-Messages}{\textbf{until} $B^{r,\textrm{pv}}_v \geqslant L$ \and $($ Time $\geqslant t_{r_,v} + 4 \times T$ \or $r$ \textbf{is} completable $)$}
    \STATE \call{Broadcast}{$M_v^{r, \textrm{pc}}(B_v^{r, \textrm{pv}})$}
    
    \REPEAT
      \STATE \call{Receive-Messages}{}
      \STATE \call{Attempt-To-Finalize-At-Round}{$r$}
    \UNTIL{$r$ \textbf{is} completable \and \call{Finalizable}{$r$} \and \textsc{Last-Finalized-Block} $\geqslant$ \call{Best-Final-Candidate}{$r - 1$}}
    
    \STATE \call{Play-Grandpa-round}{$r + 1$}
    
    \REPEAT
      \STATE \call{Receive-Messages}{}
      \STATE \call{Attempt-To-Finalize-At-Round}{$r$}
    \UNTIL{\textsc{Last-Finalized-Block} $\geqslant$ \call{Best-Final-Candidate}{$r$}}
    
    \IF{$r > $ \textsc{Last-Completed-Round}}
      \STATE \textsc{Last-Completed-Round} $\leftarrow r$
    \ENDIF
\end{algorithmic}
\end{algorithm}

where

• ${T}$ is sampled from a log-normal distribution whose mean and standard deviation are equal to the average network delay for a message to be sent and received from one validator to another.

• $\text{Derive-Primary}$ is described in Derive-Primary.

• The condition of completablitiy is defined in Definition 90.

• $\text{Best-Final-Candidate}$ function is explained in Best-Final-Candidate.

• $\text{Attempt-To-Finalize-At-Round}{\left({r}\right)}$ is described in Attempt-To-Finalize-At-Round.

• $\text{Finalizable}$ is defined in Finalizable.

Algorithm 15. Derive Primary

\begin{algorithm}
\caption{Derive-Primary}
\begin{algorithmic}
    \input $r$
    \return $r \bmod |\mathbb{V}|$
\end{algorithmic}
\end{algorithm}

where ${r}$ is the GRANDPA round whose primary is to be determined.

Algorithm 16. Best Final Candidate

\begin{algorithm}
\caption{Best-Final-Candidate}
\begin{algorithmic}
    \input $r$
    \state $B_v^{r, pv} \leftarrow$ \call{GRANDPA-GHOST}{$r$}
    \if{$r = 0$}
        \return $B_v^{r, pv}$
    \else
        \state $\mathcal{C} \leftarrow \{ B' | B' \leqslant B_v^{r,pv} | \#V^{r, pc}_{\operatorname{obv}(v), pot}(B') > \frac{2}{3} |\mathbb{V}| \}$
        \if{$\mathcal{C} = \phi$}
            \return $B_v^{r, pv}$
        \else
            \return $E \in \mathcal{C} : H_n (E) = \operatorname{max}\left(H_n (B') | B' \in \mathcal{C}\right)$
        \endif
    \endif
\end{algorithmic}
\end{algorithm}

where $\#{{V}_{{\text{obv}{\left({v}\right)},{p}{o}{t}}}^{{{r},{p}{c}}}}$ is defined in Definition 88.

Algorithm 17. GRANDPA GHOST

\begin{algorithm}
\caption{GRANDPA-GHOST}
\begin{algorithmic}
    \input $r$
    \if{$r = 0$}
        \state $G \leftarrow B_{last}$
    \else
        \state $L \leftarrow$ \call{Best-Final-Candidate}{$r - 1$}
        \state $\mathcal{G} = \{ \forall B > L | \#V_{\operatorname{obs}(v)}^{r, pv}(B) \geqslant \frac{2}{3} |\mathbb{V}| \}$
        \if{$\mathcal{G} = \phi$}
            \state $G \leftarrow L$
        \else
            \state $G \in \mathcal{G} | H_n(G) = \operatorname{max}\left( H_n (B) | \forall B \in \mathcal{G} \right)$
        \endif
    \endif
    \return $G$
\end{algorithmic}
\end{algorithm}

where

• ${B}_{{\text{last}}}$ is the last block which has been finalized on the chain (Definition 94).

• $\#{{V}_{{\text{obs}{\left({v}\right)}}}^{{{r},{p}{v}}}}{\left({B}\right)}$ is defined in Definition 87.

Algorithm 18. Best PreVote Candidate

\begin{algorithm}
\caption{Best-PreVote-Candidate}
\begin{algorithmic}
    \input $r$
    \state $B^{r, pv}_v \leftarrow$ \call{GRANDPA-GHOST}{$r$}
    \if{\call{Received}{$M_{v_{primary}}^{r, prim}(B))$ \and $B^{r, pv}_v \geqslant B > L$}}
        \state $N \leftarrow B$
    \else
        \state $N \leftarrow B^{r, pv}_v$
    \endif
\end{algorithmic}
\end{algorithm}

Algorithm 19. Attempt To Finalize At Round

\begin{algorithm}
\caption{Attempt-To-Finalize-At-Round}
\begin{algorithmic}
    \REQUIRE($r$)
    \STATE $L \leftarrow$ \textsc{Last-Finalized-Block}
    \STATE $E \leftarrow$ \call{Best-Final-Candidate}{$r$}
    \IF{$E \geqslant L$ \and ${V^{r, \textrm{pc}}_{\textrm{obs}(v)}}(E) > 2 / 3 |\mathbb{V}|$}
    \STATE{\textsc{Last-Finalized-Block}$\leftarrow E$}
    \IF{$M_v^{r, \textrm{Fin}} (E) \notin $\textsc{Received-Messages}}
        \STATE \call{Broadcast}{$M_v^{r, \textrm{Fin}}(E)$}
        \RETURN
    \ENDIF
    \ENDIF
\end{algorithmic}
\end{algorithm}

Algorithm 20. Finalizable

\begin{algorithm}
\caption{Finalizable}
\begin{algorithmic}
    \REQUIRE($r$)
    \IF{$r$ \textbf{is not} Completable}
        \RETURN \textbf{False}
    \ENDIF
    \STATE $G \leftarrow$ \call{GRANDPA-GHOST}{$J^{r, pv}(B)$}
    \IF{$G = \phi$}
        \RETURN \textbf{False}
    \ENDIF
    \STATE $E_r \leftarrow$ \call{Best-Final-Candidate}{$r$}
    \IF{$E_r \neq \phi$ \and \call{Best-Final-Candidate}{$r - 1$} $\leqslant E_r \leqslant G$}
        \RETURN \textbf{True}
    \ELSE
        \RETURN \textbf{False}
    \ENDIF
\end{algorithmic}
\end{algorithm}

where the condition for completability is defined in Definition 90.

Note that we might not always succeed in finalizing our best candidate due to the possibility of equivocation. We might even not finalize anything in a round (although Play-Grandpa-Round prevents us from moving to the round ${r}+{1}$ before finalizing the best final candidate of round ${r}-{1}$) The example in Definition 92 serves to demonstrate a situation where the best final candidate of a round cannot be finalized during its own round:

Definition 92. Unfinalized Candidate

Let us assume that we have 100 voters and there are two blocks in the chain (${B}_{{1}}<{B}_{{2}}$). At round 1, we get 67 pre-votes for ${B}_{{2}}$ and at least one pre-vote for ${B}_{{1}}$ which means that $\text{GRANDPA-GHOST}{\left({1}\right)}={B}_{{2}}$.

Subsequently, potentially honest voters who could claim not seeing all the pre-votes for ${B}_{{2}}$ but receiving the pre-votes for ${B}_{{1}}$ would pre-commit to ${B}_{{1}}$. In this way, we receive 66 pre-commits for ${B}_{{1}}$ and 1 pre-commit for ${B}_{{2}}$. Henceforth, we finalize ${B}_{{1}}$ since we have a threshold commit (67 votes) for ${B}_{{1}}$.

At this point, though, we have ${\mathtt{\text{Best-Final-Candidate}}}{\left({r}\right)}={B}_{{2}}$ as $\#{{V}_{{\text{obs}{\left({v}\right)},\text{pot}}}^{{{r},\text{stage}}}}{\left({B}_{{2}}\right)}={67}$ and ${2}>{1}$.

However, at this point, the round is already completable as we know that we have ${\mathtt{\text{GRANDPA-GHOST}}}{\left({1}\right)}={B}_{{2}}$ as an upper limit on what we can finalize and nothing greater than ${B}_{{2}}$ can be finalized at ${r}={1}$. Therefore, the condition of Play-Grandpa-Round is satisfied and we must proceed to round 2.

Nonetheless, we must continue to attempt to finalize round 1 in the background as the condition of Attempt-To-Finalize-At-Round has not been fulfilled.

This prevents us from proceeding to round 3 until either:

• We finalize ${B}_{{2}}$ in round 2, or

• We receive an extra pre-commit vote for ${B}_{{1}}$ in round 1. This will make it impossible to finalize ${B}_{{2}}$ in round 1, no matter to whom the remaining pre-commits are going to be cast for (even with considering the possibility of 1/3 of voter equivocating) and therefore we have ${\mathtt{\text{Best-Final-Candidate}}}{\left({r}\right)}={B}_{{1}}$.

Both scenarios unblock Play-Grandpa-Round, ${\mathtt{\text{Last-Finalized-Block}}}\ge{\mathtt{\text{Best-Final-Candidate}}}{\left({r}-{1}\right)}$ albeit in different ways: the former with increasing the ${\mathtt{\text{Last-Finalized-Block}}}$ and the latter with decreasing ${\mathtt{\text{Best-Final-Candidate}}}{\left({r}-{1}\right)}$.

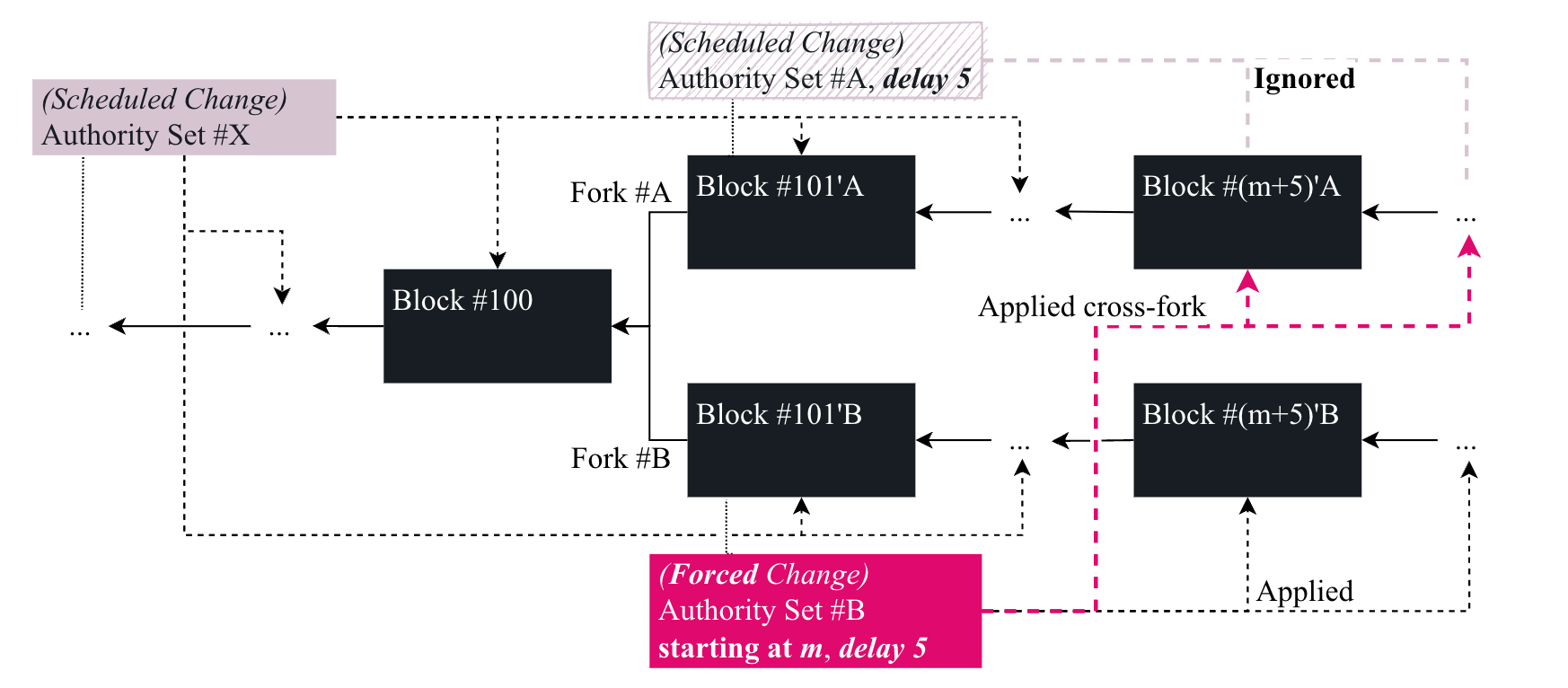
6.5. Forced Authority Set Changes

In a case of emergency where the Polkadot network is unable to finalize blocks, such as in the event of a mass validator outage, the Polkadot governance mechanism must enact a forced change, which the Host must handle in a specific manner. Given that in such a case, finality cannot be relied on, the Host must detect the forced change (Definition 91) in a (valid) block and apply it to all forks.

The ${m}\in{C}{M}_{{g}}$, which is specified by the governance mechanism, defines the starting block at which ${N}_{{\text{delay}}}$ is applied. This provides some degree of probabilistic consensus to the network with the assumption that the forced change was received by most participants and that finality can be continued.

Image 6. Applying a scheduled change

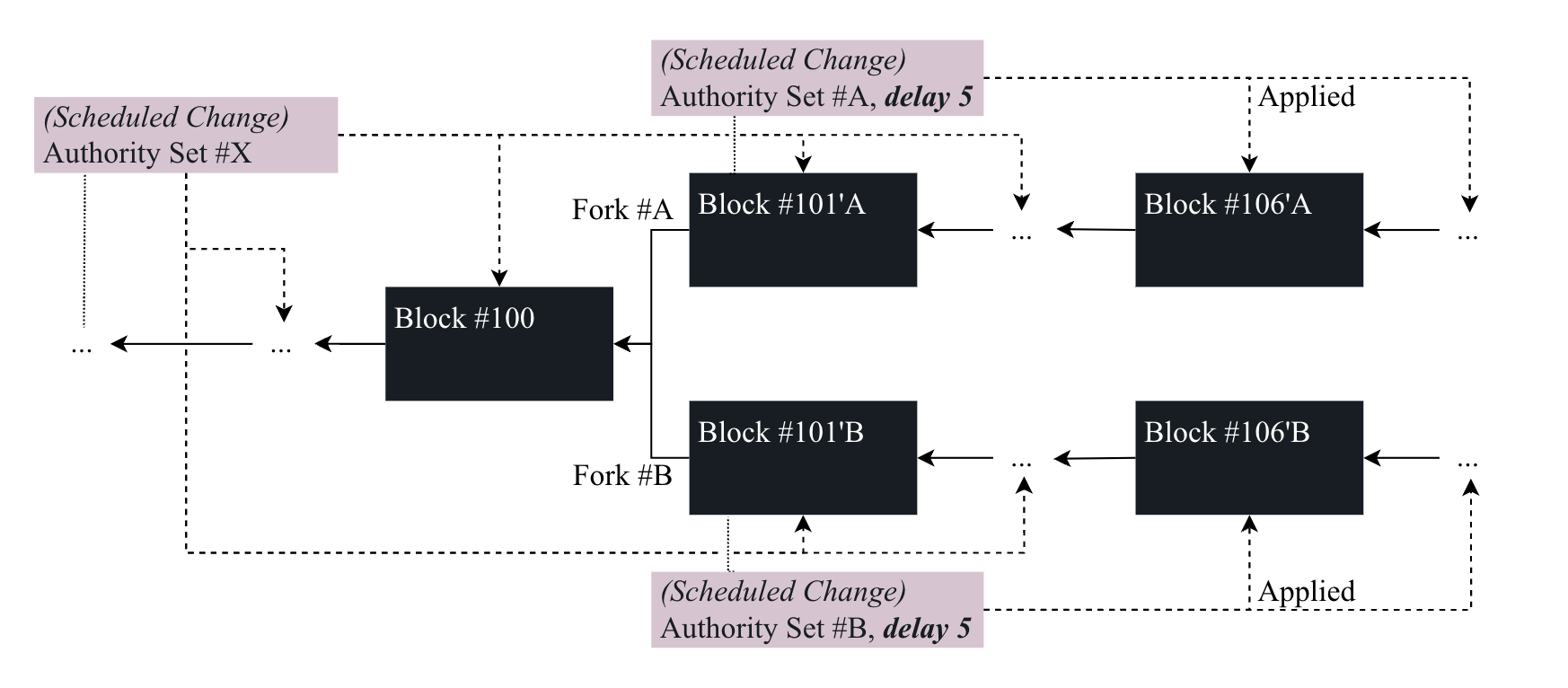
Image 7. Applying a forced change

6.6. Block Finalization

Definition 93. Justified Block Header

The Justified Block Header is provided by the consensus engine and presented to the Polkadot Host for the block to be appended to the blockchain. It contains the following parts:

• block_header the complete block header (Definition 10) and denoted by $\text{Head}{\left({B}\right)}$.

• justification: as defined by the consensus specification indicated by $\text{Just}{\left({B}\right)}$ as defined in Definition 83.

• authority Ids: This is the list of the IDs of authorities which have voted for the block to be stored and is formally referred to as ${A}{\left({B}\right)}$. An authority ID is 256-bit.

Definition 94. Finalized

A Polkadot relay chain node ${n}$ should consider block ${B}$ as finalized if any of the following criteria hold for ${B}'\ge{B}$:

• ${{V}_{{\text{obs}{\left({n}\right)}}}^{{{r},\text{pc}}}}{\left({B}'\right)}>\frac{{2}}{{3}}{\left|{\mathbb{{V}}}_{{{B}'}}\right|}$.

• It receives a ${{M}_{{v}}^{{{r},\text{Fin}}}}{\left({B}'\right)}$ message in which ${J}^{{r}}{\left({B}\right)}$ justifies the finalization (Definition 83).

• It receives a block data message for ${B}'$ with $\text{Just}{\left({B}'\right)}$ (Definition 93) which justifies the finalization.

for:

• Any round ${r}$ if the node ${n}$ is not a GRANDPA voter.

• Only for round ${r}$ for which the node ${n}$ has invoked Play-Grandpa-Round and round ${r}+{1}$ if ${n}$ is a GRANDPA voter and has already caught up to its peers according to the process described in Section Section 6.6.1..

Note that all Polkadot relay chain nodes are supposed to process GRANDPA commit messages regardless of their GRANDPA voter status.

6.6.1. Catching up

When a Polkadot node (re)joins the network, it requests the history of state transitions in the form of blocks, which it is missing.

Nonetheless, the process is different for a GRANDPA voter node. When a voter node joins the network, it needs to gather the justification (Definition 83) of the rounds it has missed. Through this process, they can safely join the voting process of the current round, on which the voting is taking place.

6.6.1.1. Sending the catch-up requests

When a Polkadot voter node has the same authority list as a peer voter node who is reporting a higher number for the finalized round field, it should send a catch-up request message (Definition 53) to the reporting peer. This will allow the node to to catch up to the more advanced finalized round, provided that the following criteria hold:

• The peer node is a GRANDPA voter, and:

• The last known finalized round for the Polkadot node is at least two rounds behind the finalized round for the peer.

6.6.1.2. Processing the catch-up requests

Only GRANDPA voter nodes are required to respond to the catch-up requests. Additionally, it is only GRANDPA voters who are supposed to send catch-up requests. As such GRANDPA voters could safely ignore the catch-up requests from non-voter nodes. When a GRANDPA voter node receives a catch-up request message, it needs to execute Process-Catchup-Request. Note: a voter node should not respond to catch-up requests for rounds that are actively being voted on. Those are the rounds for which Play-Grandpa-Round is not concluded.

Algorithm 21. Process Catchup Request

\begin{algorithm}
\caption{Process-Catchup-Request}
\begin{algorithmic}
    \input $M_{i, v}^\text{Cat-q}(\text{id}_\mathbb{V}, r)$
    \if{$M_{i, v}^\text{Cat-q}(\text{id}_\mathbb{V}, r).\text{id}_\mathbb{V} \neq \text{id}_\mathbb{V}$}
        \state \textbf{error} ``Catching up on different set''
    \endif
    \if{$i \notin \mathbb{P}$}
        \state \textbf{error} ``Requesting catching up from a non-peer''
    \endif
    \if{$r >$ \textsc{Last-Completed-Round}}
        \state \textbf{error} ``Catching up on a round in the future''
    \endif
    \state \call{Send}{$i, M_{v, i}^\text{Cat-s}(\text{id}_\mathbb{V}, r)$}
\end{algorithmic}
\end{algorithm}

where

• ${{M}_{{{i},{v}}}^{{\text{Cat}-{q}}}}{\left(\text{id}_{{{\mathbb{{V}}}}},{r}\right)}$ is the catch-up message received from peer ${i}$ (Definition 53).

• $\text{id}_{{{\mathbb{{V}}}}}$ (Definition 78) is the voter set id with which the serving node is operating

• ${r}$ is the round number for which the catch-up is requested for.

• ${\mathbb{{P}}}$ is the set of immediate peers of node ${v}$.

• ${\mathtt{\text{Last-Completed-Round}}}$ is initiated in Initiate-Grandpa and gets updated by Play-Grandpa-Round.

• ${{M}_{{{v},{i}}}^{{\text{Cat}-{s}}}}{\left(\text{id}_{{{\mathbb{{V}}}}},{r}\right)}$ is the catch-up response (Definition 54).

6.6.1.3. Processing catch-up responses

A Catch-up response message contains critical information for the requester node to update their view on the active rounds that are being voted on by GRANDPA voters. As such, the requester node should verify the content of the catch-up response message and subsequently updates its view of the state of the finality of the Relay chain according to Process-Catchup-Response.

Algorithm 22. Process Catchup Response

\begin{algorithm}
\caption{Process-Catchup-Response}
\begin{algorithmic}
    \input $M_{v,i}^\text{Cat-s}(\text{id}_{\mathbb{V}}, r)$
    \state $M_{v,i}^\text{Cat-s}(\text{id}_{\mathbb{V}}, r).\text{id}_{\mathbb{V}}, r, J^{r, pv}(B), J^{r, pc}(B), H_h(B'), H_i(B') \leftarrow \text{Dec}_{SC}(M_{v, i}^{Cat-s}(\text{id}_{\mathbb{V}}, r)$
    \if{$M_{v, i}^\text{Cat-s}(\text{id}_{\mathbb{V}}, r).\text{id}_{\mathbb{V}} \neq \text{id}_{\mathbb{V}}$}
        \state \textbf{error} ``Catching up on different set''
    \endif
    \if{$r \leqslant$ \textsc{Leading-Round}}
        \state \textbf{error} ``Catching up in to the past''
    \endif
    \if{$J^{r, pv}(B)$ \textbf{is not} valid}
        \state \textbf{error} ``Invalid pre-vote justification''
    \endif
    \if{$J^{r, pc}(B)$ \textbf{is not} valid}
        \state \textbf{error} ``Invalid pre-commit justification''
    \endif
    \state $G \leftarrow$ \call{GRANDPA-GHOST}{$J^{r, pv}(B)$}
    \if{$G = \phi$}
        \state \textbf{error} ``GHOST-less Catch-up''
    \endif
    \if{$r$ \textbf{is not} completable}
        \state \textbf{error} ``Catch-up round is not completable''
    \endif
    \if{$J^{r, pc}(B)$ justifies $B'$ finalization}
        \state \textbf{error} ``Unjustified Catch-up target finalization''
    \endif
    \state \textsc{Last-Completed-Round} $\leftarrow r$
    \if{$i \in \mathbb{V}$}
        \state \call{Play-Grandpa-round}{$r + 1$}
    \endif
\end{algorithmic}
\end{algorithm}

where ${{M}_{{{v},{i}}}^{{\text{Cat}-{s}}}}{\left(\text{id}_{{{\mathbb{{V}}}}},{r}\right)}$ is the catch-up response received from node ${v}$ (Definition 54).

6.7. Bridge design (BEEFY)

The BEEFY (Bridge Efficiency Enabling Finality Yielder) is a secondary protocol to GRANDPA to support efficient bridging between the Polkadot network (relay chain) and remote, segregated blockchains, such as Ethereum, which were not built with the Polkadot interchain operability in mind. BEEFY’s aim is to enable clients to efficiently follow a chain that has GRANDPA finality, a finality gadget created for Substrate/Polkadot ecosystem. This is useful for bridges (e.g., Polkadot->Ethereum), where a chain can follow another chain and light clients suitable for low storage devices such as mobile phones.

The protocol allows participants of the remote network to verify finality proofs created by the Polkadot relay chain validators. In other words: clients in the target network (e.g., Ethereum) can verify that the Polkadot network is at a specific state.

Storing all the information necessary to verify the state of the remote chain, such as the block headers, is too expensive. BEEFY stores the information in a space-efficient way, and clients can request additional information over the protocol.

6.7.1. Motivation

A client could just follow GRANDPA using GRANDPA justifications, sets of signatures from validators. This is used for some substrate-substrate bridges and in light clients such as the Substrate Connect browser extension. GRANDPA was designed for fast and secure finality. Certain design decisions, like validators voting for different blocks in a justification and using ED25519 signatures, allow fast finality. However, GRANDPA justifications are large and are expensive to verify on other chains like Ethereum that do not support some cryptographic signature schemes. Thus, BEEFY adds an extra layer of finality that allows lighter bridges and clients for Polkadot.

To summarise, the goals of BEEFY are:

• Allow customization of signature schemes to adapt to different target chains.
• Minimize the size of the finality proof and the effort required by a light client to follow finality.
• Unify data types and use backward-compatible versioning so that the protocol can be extended (additional payload, different signature schemes) without breaking existing light clients.

6.7.2. Protocol Overview

Since BEEFY runs on top of GRANDPA, similarly to how GRANDPA is lagging behind the best produced (non-finalized) block, BEEFY finalized block lags behind the best GRANDPA (finalized) block.

• The BEEFY validator set is the same as GRANDPA's. However, they might be using different types of session keys to sign BEEFY messages.
• From a single validator perspective, BEEFY has at most one active voting round.
• Since GRANDPA validators are reaching finality, we assume they are online and well-connected and have a similar view of the state of the blockchain.

BEEFY consists of two components:

a. Consensus Extension on GRANDPA finalization that is a voting round.

The consensus extension serves to have a smaller consensus justification than GRANDPA and alternative cryptography, which helps the light client side of the BEEFY protocol described below.

b. An efficient protocol for convincing on-chain/ off-chain light clients about the finality vote.

In the BEEFY light-client protocol, a full node or bridge relayer (prover) wants to convince a light client (verifier, e.g., a smart contract implemented on the target chain) of the outcome of BEEFY votes. The prover has access to all voting data from the BEEFY voting round. The prover may generate a single-shot proof (for e.g. using SNARKS) and send it to the verifier or they may engage in an interactive protocol with several rounds of communication.

6.7.3. Preliminaries

Definition 95. BEEFY Session Keys

Validators use an ECDSA key scheme for signing Beefy messages. This is different from schemes like sr25519 and ed25519, which are commonly used in Substrate for other components like BABE, and GRANDPA. The most noticeable difference is that an ecdsa public key is 33 bytes long, instead of 32 bytes for a sr25519 based public key. As a consequence, the AccountId (32-bytes) matches the PublicKey for other session keys, but note that it's not the case for BEEFY.

BEEFY session key pair ${\left({s}{{k}_{{j}}^{B}},{p}{{k}_{{j}}^{B}}\right)}$ is a secp256k1 key pair which the BEEFY authority node ${\mathcal{{P}}}_{{j}}$ uses to sign the BEEFY signed commitments (justifications).

6.7.4. Merkle Mountain Ranges

Definition 96. Merkle Mountain Ranges

Merkle Mountain Ranges, MMR, are used as an efficient way to send block headers and signatures to light clients. Merkle Mountain Ranges (MMR) is an improvement of the traditional Merkle tree data structure. Just like a Merkle tree, an MMR is a binary tree where each leaf node represents a data element and each non-leaf node is the hash of its child nodes. The key difference between a traditional Merkle tree and a MMR lies in the way nodes are organized. In traditional Merkle trees, whenever a leaf node is appended or removed, the tree must be rebuilt and the hashes of the non-leaf nodes must be recalculated. The overhead of recomputing the hashes up to the root makes traditional Merkle unsuitable for handling dynamic data. The MMR is designed to optimize the appending and removal of elements without requiring a complete rebuild of the tree, which makes it more efficient to handle growing lists of leaf nodes.

MMR structure

A MMR structure can be seen as a list of perfectly balanced binary sub-trees in descending order of height. It is a strictly append-only structure where nodes are added from left to right, such that a parent node is added as soon as two children exist. The following representation shows a MMR with 11 elements, 7 leaf nodes and 4 non-leaf nodes, where the value of each node corresponds to the order in which it was inserted into the tree.

       7
      / \
     /   \
    /     \
   3       6        10
  / \     / \       / \   
 /   \   /   \     /   \   
1     2 4     5   8     9    11

Definition 97. Merkle Mountain Ranges root (MMR-root)

An MMR does not have a single root by design, as a conventional Merkle tree. Every sub-tree has a separate sub-root, which we refer to as the peak of the sub-tree. Bagging the peaks is the process used for hashing the peaks in order to compute the MMR-root. It is important to define the order in which the peaks are hashed to ensure that a given sub-set of peaks will always derive a unique MMR-root. Here we state that peaks are merged from right to left and bagged via $hash(right, left)$.

Therefore, given an MMR tree with n peaks ordered in decreasing order of height, the MMR-root of the tree is calculated as follows.

$$\texttt{MMR root} = hash (p_1 + hash( p_2 + hash( p_3 +... + hash ( p_n-1 + p_n ))))$$

where

• $p_1, p_2,...,p_n$: represents the list of current peaks in decreasing order of heights.
• $hash$: corresponds to the 256-bit Keccak hash function used to merge the peaks.

A distinguished feature of this process is that whenever new leaf nodes are added to the tree, the earlier hash computations of peaks are reused, making new leaf nodes less expensive to insert and to prove (i.e., to verify the integrity of leaf data).

Definition 98. MMR operations

Here are the basic operations we should be able to perform on the MMR:

• Append Leaf Node (appendData):

  • Signature: append(data: T) -> None
  • Description: appends a new leaf element with the provided data to the MMR.

• Create MMR root (bagPeaks):

  • Signature: baggingPeaks(peaksIndexes: List[int]) -> str
  • Description: creates the single MMR root based on the list of peaks, and returns the hash string of the MMR root corresponding to the current state of the tree.

• Verify Node (verifyProof):

  • Signature: verifyNode(nodeHash: str, requiredProofNodes: List[str], MMRroot: str) -> bool
  • Description: verifies if the given node hash can be proved based on the list of required proof nodes and the MMR root hash.

Definition 99. Payload

Payload: is the Merkle root of the MMR generated where the leaf data contains the following fields for each block:

• LeafVersion: a byte indicating the current version number of the Leaf Format. The first 3 bits are for major versions and the last 5 bits are for minor versions.
• BeefyNextAuthoritySetInfo: It is a tuple consisting of:
  • ValidatorSetID
  • Len (u32): length of the validator set
  • Merkle Root of the list of Next Beefy Authority Set (ECDSA public keys). The exact format depends on the implementation.
• Parent Block number and Parent Block Hash.
• Extra Leaf Data: Currently the Merkle root of the list of (ParaID, ParaHeads)

Definition 100. Signed Commitment

Signed Commitment: commitment is a tuple of (payload, Block Number, ValidatorSetID). A signed commitment is a tuple (commitment, signatures), where signatures is a list of optional signatures of the validator set on the SCALE encoded commitment. Note that the number of signatures in signatures may be less than the length of the Validator Set.

Definition 101. Witness Data

Signed Commitment Witnesses contains the commitment and an array indicating which validator of the Polkadot network voted for the payload (but not the signatures themselves). The indicators of which validator voted for the payload are just claims and provide no proof. It also contains the signature of one validator on the commitment, which is used only by the subsampling-based Light Clients. The network message is defined in Definition 58 and the relayer saves it on the chain of the remote network.

Definition 102. Light Client

A light client is an abstract entity in a remote network such as Ethereum. It can be a node or a smart contract with the intent of requesting finality proofs from the Polkadot network. A light client reads the witness data (Definition 101 from the chain, then requests the signatures directly from the relayer in order to verify those.

Definition 103. Relayer

A relayer (or "prover") is an abstract entity that takes finality proofs from the Polkadot network and makes those available to the light clients. The relayer attempts to convince the light clients that the finality proofs have been voted for by the Polkadot relay chain validators. The relayer operates off-chain and can for example be a node or a collection of nodes.

6.7.5. Voting on Payloads

The Polkadot Host signs the MMR payload (Definition 99) and gossips it as part of a vote (Definition 56) to its peers on every new finalized block. The Polkadot Host uses ECDSA for signing the payload since Ethereum has better compatibility for it compared to SR25519 or ED25519.

6.7.6. Committing Witnesses

The relayer (Definition 103) participates in the Polkadot network by collecting the gossiped votes (Definition 56). Those votes are converted into the witness data structure (Definition 101). The relayer saves the data on the chain of the remote network. The occurrence of saving witnesses on remote networks is undefined.

6.7.7. Requesting Signed Commitments

A light client (Definition 102) fetches the Signed Commitment Witness (Definition 101) from the chain. Once the light client knows which validators apparently voted for the specified payload, it needs to request the signatures from the relayer to verify whether the claims are actually true. This is achieved by requesting signed commitments (Definition 57).

How those signed commitments are requested by the light client and delivered by the relayer varies among networks or implementations.

Definition 104. BEEFY Consensus Message

$\text{CM}_{{beefy}}$, the consensus message for BEEFY, is of the following format:

$$\text{CM}_{{beefy}}={\left\lbrace\begin{matrix}{1}&{\left({V}_{{B}},{V}_{{i}}\right)}\\{2}&{A}_{{i}}\\{3}&{R}\end{matrix}\right.}$$

where

1	implies that the remote authorities have changed. ${V}_{{B}}$ is the array of the new BEEFY authorities’s public keys and ${V}_{{i}}$ is the identifier of the remote validator set.
2	implies on disabled: an index to the individual authority in ${V}_{{B}}$ that should be immediately disabled until the next authority change.
3	implies MMR root: a 32-byte array containing the MMR root payload.

6.7.8. Consensus Mechanism

Role of various Actors in BEEFY:

• Validators are expected to additionally:

  1. Produce & broadcast vote for the current round.

• Regular nodes perform the following tasks:

  1. Receive & validate votes for the current round and broadcast them to their peers.
  2. Receive & validate BEEFY Justifications and broadcast them to their peers.
  3. Return BEEFY Justifications for Mandatory Blocks on demand.
  4. Optionally return BEEFY Justifications for non-mandatory blocks on demand.

A round is an attempt by BEEFY validators to produce a BEEFY Justification. Round number is simply defined as a block number the validators are voting for, or to be more precise, the Commitment for that block number. Round ends when the next round is started, which may happen when one of the events occur:

1. Either the node collects 2/3rd + 1 valid votes for that round.
2. Or the node receives a BEEFY Justification for a block greater than the current best BEEFY block.

In both cases the node proceeds to determine the new round number using "Round Selection" procedure.

Both kinds of actors are expected to fully participate in the protocol ONLY IF they believe they are up-to-date with the rest of the network, i.e. they are fully synced. Before this happens, the node should continue processing imported BEEFY Justifications and votes without actively voting themselves.

Round Selection

Every node (both regular nodes and validators) determines locally what it believes the current round number is. The choice is based on their knowledge of:

1. Best GRANDPA finalized block number (best_grandpa).
2. Best BEEFY finalized block number (best_beefy).
3. Starting block of the current session (session_start).

Session means a period of time (or rather a number of blocks) where the validator set (keys) does not change. Session are synonymous to epochs (Definition 59). Since the BEEFY authority set is the same as the GRANDPA authority set for any GRANDPA finalized block, the session boundaries for BEEFY are exactly the same as the ones for GRANDPA.

We define two kinds of blocks from the perspective of the BEEFY protocol:

1. Mandatory Blocks
2. Non-mandatory Blocks

Mandatory blocks are the ones that MUST have BEEFY justification. That means that the validators will always start and conclude a round at mandatory blocks. For non-mandatory blocks, there may or may not be a justification and validators may never choose these blocks to start a round.

Every first block in each session is considered a mandatory block. All other blocks in the session are non-mandatory, however validators are encouraged to finalize as many blocks as possible to enable lower latency for light clients and hence end users. Since GRANDPA is considering session boundary blocks as mandatory as well, session_start block will always have both GRANDPA and BEEFY Justification.

Definition 105. BEEFY Round NUmber

The formula for determining the current round number is defined as:

round_number =
      (1 - M) * session_start
   +        M * Minimum(next_session_start, (best_beefy + NEXT_POWER_OF_TWO((best_grandpa - best_beefy + 1) / 2)))

where:

• M is 1 if the mandatory block in the current session is already finalized and 0 otherwise.
• NEXT_POWER_OF_TWO(x) returns the smallest number greater or equal to x that is a power of two.

Intuitively, the next round number should be the oldest mandatory block without a justification, or the highest GRANDPA-finalized block, whose block number difference with best_beefy block is a power of two. The mental model for round selection is to first finalize the mandatory block and then to attempt to pick a block taking into account how fast BEEFY catches up with GRANDPA. In case GRANDPA makes progress, but BEEFY seems to be lagging behind, validators are changing rounds less often to increase the chance of concluding them.

As mentioned earlier, every time the node picks a new round_number (and the validator casts a vote) it ends the previous one, no matter if finality was reached (i.e. the round concluded) or not. Votes for an inactive round should not be propagated.

Note that since BEEFY only votes for GRANDPA-finalized blocks, session_start here actually means: "the latest session for which the start of is GRANDPA-finalized", i.e. block production might have already progressed, but BEEFY needs to first finalize the mandatory block of the older session.

While it is useful to finalize non-mandatory blocks frequently, in good networking conditions BEEFY may end up finalizing each and every block GRANDPA finalized block. Practically, with short block times, it's going to be rare and might be excessive, so it's suggested for implementations to introduce a min_delta parameter which will limit the frequency with which new rounds are started. The affected component of the formula would be: best_beefy + MAX(min_delta, NEXT_POWER_OF_TWO(...)), so we start a new round only if the the power-of-two component is greater than the min delta. Note that if round_number > best_grandpa the validators are not expected to start any round.

6.7.9. BEEFY Light Client

A light client following BEEFY could request $N/3 +1$ signatures to be checked, where $N$ is the number of validators on Polkadot. Assuming a maximum of $N/3$ malicious validators, the light client can be certain of the payloads finality if all the signatures it requested are valid.

6.7.10. Subsampling Light Client

It is an interactive protocol between the light-client (verifier) and the relayer (prover) to convince the Light Client with a high probability that the payload sent by the prover is signed by honest Polkadot validators. The protocol prioritizes efficiency and tries to minimize the number ($<< N/3$) of signature checks (computationally expensive operations) on the light client side.

6.7.11. APK Proof based Light Clients

TODO: Section on using Aggregatable Signatures for efficient verification on light clients.